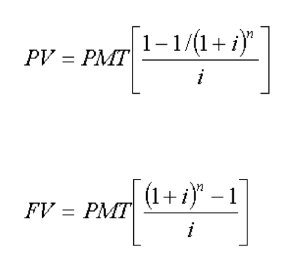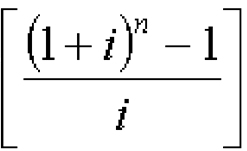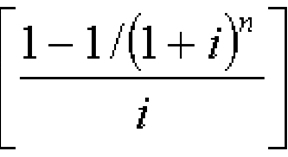¬ Lição matemática nº13: Como calcular o tamanho da amostra em uma pesquisa

Geralmente associamos um número muito grande de entrevistados (amostra) com uma maior precisão no que concluiremos sobre a população. Todavia, a estatística nos mostra que pequenas amostras nos dão resultados precisos. Até porque, mesmo pequena, quando planejada e coletada de forma científica, terá resultados mais precisos do que amostras muito grandes e sem critérios técnicos. A questão então não é o tamanho da amostra, mas a cientificidade, o tratamento estatístico que ela recebe. Ademais, grandes amostras geram um problema adicional, os erros não amostrais, causados por motivos como: o modo equivocado de coleta dos dados, influência dos pesquisadores, etc. Esses erros não amostrais ficam muito mais difíceis de serem controlados ou minimizados, tendendo a crescer, portanto, na medida em que o tamanho da amostra aumenta. Além disso, a partir de certo número de entrevistas, é necessário aumentar muito o tamanho da amostra para conseguir diminuir muito pouco a margem de erro da pesquisa, ou seja, seria necessário aumentar muito os custos para obter poucos benefícios. Portanto, ao contrário do senso comum, o tamanho da amostra depende parcialmente do tamanho da população, e mais do tratamento estatístico que recebe.

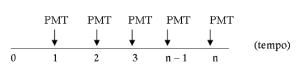
Mas, as inferências (conclusões) a partir da média de uma amostra de uma população são realmente confiáveis para retratar a média de toda a população? Vejamos o exemplo a seguir (adaptado de Fauze Mattar, em Pesquisa de Marketing). Imaginemos uma população de 10 indivíduos, cujos salários sejam os seguintes:

Indivíduos	Salários
João	$1.300
Maria	$1.300
Pedro	$1.400
Marcos	$1.500
Mateus	$1.600
Flávia	$1.600
Lupicínio	$1.700
Washington	$1.800
Carina	$1.900
Juliana	$1.900
TOTAL	$16.000
Renda média da população	$1.600

Selecionando aleatoriamente uma amostra de 2 indivíduos teríamos as seguintes possibilidades, combinações, de amostras:

Nº da amostra	Amostra	Renda média da amostra de 2 indivíduos
1	João e Maria	R$ 1.300,00 = (1.300 +1.300)/2
2	João e Pedro	R$ 1.350,00
3	João e Marcos	R$ 1.400,00
4	João e Mateus	R$ 1.450,00
5	João e Flávia	R$ 1.450,00
..	...	...
40	Lupicínio e Washington	R$ 1.750,00
41	Lupicínio e Carina	R$ 1.800,00
42	Lupicínio e Juliana	R$ 1.800,00
43	Washington e Carina	R$ 1.850,00
44	Washington e Juliana	R$ 1.850,00
45	Carina e Juliana	R$ 1.900,00
	Total das médias das amostras	R$ 72.000,00
	Média da média das amostras	R$ 1.600 (72.000/45)

Concluímos, portanto, que se todas as amostras possíveis fossem selecionadas, 45 no total, e tirada a média de cada uma delas, a média geral de todas essas médias das amostras seria exatamente, e obrigatoriamente, igual à média da população. Uma tabela de freqüências dos salários médios das amostras de tamanho ficaria assim distribuída:

Média das amostras	Frequência
$1.300	1
$1.350	2
$1.400	2
$1.450	5
$1.500	4
$1.550	5
$1.600	7
$1.650	5
$1.700	4
$1.750	5
$1.800	2
$1.850	2
$1.900	1
Total	45

Notamos que, assim como a média, a mediana e a moda também foram de R$1.600. Conclusões que tiramos do exemplo anterior:

  
• A média da população é efetivamente IGUAL à média da média das amostras individuais

• As médias das amostras estão distribuídas em torno da média da população (R$1.600), sendo que 7 médias amostrais (a moda) são exatamente iguais a média da população;


• As frequências dos valores mais próximos à media da população tendem a ser maiores do que os mais distantes. Os salários médios de $1.650 e $1.550, por exemplo, possuem 5 repetições (freqüências) cada. Já os salários médios de $1.300 e $1.900 acontecem apenas 1 vez cada.


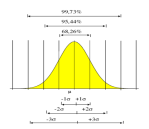
• A forma do gráfico dessa distribuição de freqüências das amostras assume o formato de uma curva na forma de sino em torno da média da população ($1.600), como vemos na figura abaixo. Essa curva é denominada CURVA NORMAL, como vimos na lição anterior.

  

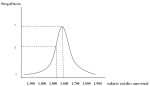
Se no caso anterior, para uma população de 10 indivíduos, amostras de dois indivíduos resultaram em 45 possibilidades imaginem uma amostra com 600!? A estatística tenta resolver esse problema, ou seja, dar representatividade à população a partir da média de apenas uma amostra de 600 selecionada aleatoriamente, evitando o que seria impossível, tirar a média de todas as outras milhares de amostras com 600 indivíduos.

O que fazer então? Voltando ao nosso exemplo acima, trabalhando com apenas 1 amostra, dentre as 45 amostras possíveis de 2 indivíduos, temos que considerar que pequenos erros (desvios) são possíveis quando comparados com as outras 44 médias das amostras – esses erros são os erros amostrais. Isto porque essa única amostra pode resultar em quaisquer valores entre R$1.300 e R$1.900. Logo, ela não representará fielmente a média da população, pois só encontramos exatamente R$1.600, que é a verdadeira média da população, quanto utilizamos todas as 45 médias amostrais. Ou seja, os resultados obtidos numa pesquisa elaborada a partir de amostras não são rigorosamente exatos em relação ao universo. Esses resultados apresentam sempre um erro de medição. Detalhemos, então, o conceito de erro amostral e outros conceitos inerentes às pesquisas: intervalo de confiança e nível de confiança.

Como vimos, o erro amostral é a diferença entre o valor da amostra selecionada, dentre todas as amostras possíveis (45 no nosso exemplo), e o valor real da média de todas as amostras (R$1.600), que é a própria média da população.

A estimativa desse intervalo onde se encaixam os possíveis resultados das amostras é denominado de intervalo de confiança, que inclui a média da amostra mais o erro amostral tolerável para mais ou para menos, sendo esse erro medido em desvios padrão. Além de declarar o tamanho do intervalo, é costume declarar a probabilidade (certeza) que esse intervalo de confiança inclua o valor real, média real, da população. Essa probabilidade é conhecida como nível de confiança.

 Ou seja, 95,5% de nível de confiança significa 95,5% de ‘segurança’ (probabilidade) de que a média real da população recaia no intervalo (intervalo de confiança) que fica entre a média da amostra calculada mais (ou menos) o erro amostral aceito.

erro amostral aceito – (média da amostra) + erro amostral aceito

  (em desvios padrão)                                      (em desvios padrão)

confiança de 68,3%, 95,5% ou 99,7% de que  a média da população caia neste intervalo

Já vimos, quando tratamos do desvio padrão, que estudos estatísticos mostram que 68,3% dos indivíduos da amostra ficam entre a média da amostra mais 1 desvio padrão, para mais ou para menos. Ou seja, há uma probabilidade, nível de confiança, de 68,3% de que a média da amostra fique dentro de um erro-padrão (desvio-padrão), para mais ou para menos, da média real da população. Da mesma forma, há um nível de confiança de 95,5% de que o valor real da população é igual à estimativa da amostra mais ou menos dois erros-padrão, e 99,7% de confiança de que o valor real da população se enquadre dentro do intervalo definido pelo valor da amostra mais ou menos 3 erros-padrão (desvios-padrão).

 Logo, quanto maior o erro tolerável, em desvios padrão, maior será a confiança de que o valor da amostra represente o valor real da população, já que ao incluir uma margem de erro amostral muito grande acabamos englobando boa parte dos diversos valores que as várias amostragens sucessivas resultariam. Ou seja, para obtermos um nível de confiança de 99,7%, uma probabilidade de quase 100% de que a amostra represente o valor real da população, precisamos trabalhar com um intervalo maior (erro maior), o que encamparia boa parte das possíveis médias amostrais. Por isso os 3 desvios padrão.

Testando o raciocínio

Façamos uma demonstração a partir do nosso exemplo dos salários médios. Selecionemos apenas uma amostra de 2 indivíduos. A  média da amostra escolhida foi de R$1.600. Se calcularmos o desvio padrão dessa distribuição amostral encontramos R$143. Esse valor, como vimos no assunto desvio padrão, mostra o desvio de todos os salários (neste caso apenas 2 salários) com relação à média amostral. Para um nível de confiança de 95,5%, temos que trabalhar com um erro de 2 desvios padrão, para mais ou para menos. Considerando um salário médio de $1.600, isso resulta em um intervalo de confiança entre $1.316 a $1.886. Nesse sentido, temos uma confiança de 95,5%, de que a(s) média(s) da amostra, que será representativa da população, cairá nesse intervalo. Assim, das 45 possíveis combinações de amostragem 95,5% delas, 43 amostras, terão uma média que se encaixa dentro do intervalo de confiança e representarão o verdadeiro valor da população. Olhando para as 45 amostras percebemos que de fato apenas duas delas não caem dentro do intervalo de $1.316 a $1.886, a primeira ‘João e Maria’ ($1.300) e a última ‘Carina e Juliana’ ($1.900). Essas 43 amostras garantem, portanto, um nível de confiança de 95,5% (43/45 = 95,55%).

     $286        –             $1.600             +        $286   

(2 desvios)          (média da amostra)        (2 desvios)

Confiança de 95,5% de que a média da população  caia neste intervalo

 Fórmulas para o cálculo do tamanho da amostra

O nível de confiança e a quantidade de erro amostral (erro-padrão) devem ser estabelecidos pelo pesquisador para determinar o tamanho da amostra. Sabemos também que quanto maior a amostra menor é o erro. Assim, temos as seguintes fórmulas para o cálculo do tamanho da amostra:

Onde:

n = tamanho da amostra.

S = nível de confiança escolhido, expresso em número de desvios-padrão

p = percentagem com a qual o fenômeno se verifica - percentagem dos elementos da amostra favorável ao atributo pesquisado.

q = percentagem complementar, isto é, (100 - p) - percentagem dos elementos da amostra desfavorável

N = tamanho da população.

e = erro máximo permitido.


Exemplos:

1) Deseja-se fazer uma pesquisa para saber o consumo médio mensal, em reais, da população de determinada região. Qual é o número de pessoas que devem ser entrevistadas com 7% de erro. Considere 3 níveis de confiança: 95,5%; 68,26% e 99,7%.

Para 68,3% (1 desvio):

n = 1² x 50 x 50 / 7²

n = 51


Para 95,5% (2 desvios):

n = 2² x 50 x 50 / 7²

n = 204


Para 99,7% (3 desvios):

n = 3² x 50 x 50 / 7²

n = 460

* o resultado, consumo médio, encontrado nessa amostra de 460 entrevistados, variando essa média 7% para mais ou para menos, representa o consumo médio da população de consumidores.

Observem que o pesquisador trabalha com o mesmo erro amostral, 7%. A cada nível de confiança escolhido a variável de ajuste é o número de entrevistados (amostra). Ao elevar o nível de confiança o que acontece é uma elevação no número de entrevistados, o que garante um resultado mais preciso do resultado da pesquisa. Assim, se escolhermos um  nível de confiança de 68,3% (entrevistando 51 pessoas)  e o resultado dessa entrevista acusasse que o gasto médio dos 51 foi de R$300 a leitura seria: "concluímos que a população da cidade tem um gasto médio entre R$279 e R$321, com uma confiança, certeza, de 68,3%". Isto é, se entrevistássemos todos os indivíduos da população 68,3% deles teriam um gasto entre R$279 e R$321. Ou, para ser mais preciso, O GASTO MÉDIO DA POPULAÇÃO, se todos fossem entrevistados, FICARIA ENTRE R$279 e R$321.

Para 99,7%, considerando os mesmos 7% de erro, imaginemos que o gasto médio calculado para os 460 entrevistados fosse de R$400 (notem que coloquei um gasto médio de $400 porque agora são 460 entrevistados, e não mais 51; ou seja, coloquei um valor qualquer para mostrar que o resultado da entrevista com 460 deve ser diferente daquele com 51 indivíduos). Neste caso, leríamos: "concluímos que o gasto médio da população se situa entre R$332 e R$428, com uma confiança de 99,7%".  Isto é, se entrevistássemos todos os indivíduos da população 99,7% deles teriam um gasto entre R$332 e R$428.

Portanto, observem que o aumento na confiança é representado pelo número maior da amostra. Assim, o valor de R$400, com seu respectivo intervalo de 7% para mais ou para menos, é mais confiável, preciso, que o de R$300; e isto se dá pelo fato de termos entrevistado mais pessoas.

2) Uma empresa quer identificar quantos dos seus 10.000 empregados são sindicalizados. Presume-se que esse número não seja superior a 30% do total, deseja-se um nível de confiança de 95,5% (dois desvios) e tolera-se um erro de até 3 p.p.

n =     2² x   30  x  70   x  10.000   =  854 funcionários

            3² x 9.999 + 2² x 30 x 70

* se dos 853 funcionários entrevistados 10% forem sindicalizados concluímos que dos 10.000 empregados o percentual de sindicalizados fica entre 7% e 13%.

3) As companhias de seguro estão ficando preocupadas com o fato de que o número crescente de telefones celulares resulte em maior número de colisões de carros. Estão, por isso, pensando em cobrar prêmios mais elevados para os motoristas. Deseja-se estimar, com uma margem de erro de 3 p.p, a percentagem de motoristas que falam ao celular enquanto dirigem. Para um nível de confiança de 95% nos resultados, quantos motoristas devem ser investigados?

Suponha que não tenhamos nenhuma informação sobre p.

n = 1,96² x 50 x 50 / 3²  = 1.067 motoristas

.
* para 95,44% são 2 desvios, já para 95% (o único nível de confiança fora dos 3 citados) temos 1,96 desvios. 

.

4) O IBOPE está interessado em estimar a proporção de residências que assistem ao programa do Faustão. Qual o número mínimo de residências que se deve analisar para ter 95,5% de confiança e margem de erro máxima de 2pp para a estimativa? R: 2.500

5) Estamos interessados em determinar o tamanho da amostra necessária para estimar a proporção de eleitores que votam em certo candidato, com nível de confiança de 95% e uma margem de erro de 2pp. Quantos eleitores devem ser entrevistados? R: 2.401

6) Um colégio de Ensino médio tem 240 alunos entre as 3 séries. Os alunos devem escolher entre 2 candidatos quem será o presidente do grêmio estudantil. Qual o tamanho da amostra necessária para estimar as intenções de voto, com 95% de confiança e uma margem de erro máxima de 2p.p? Este é um problema proposto em um livro de segunda série do Ensino Médio. Lá, a resposta é 24. Qual a resposta correta? R: 218

7) Em 12/09/2008 o Instituto Futura divulgou a seguinte pesquisa de intenções de voto para a prefeitura da Serra. Qual foi o tamanho da amostra? R: 601

.

Vejam abaixo um exemplo da metodologia e o cálculo do tamanho da amostra de uma pesquisa eleitoral feita por um instituto de pesquisa em Vitória (ES).

.

METODOLOGIA (http://gazetaonline.globo.com/futuranet/)

Empresa responsável: Instituto de pesquisa Futura.

Contratante: Rede Gazeta.

Metodologia: pesquisa quantitativa.

Universo e unidade respondente: morador e eleitor do município da Serra.

Amostra: ???? entrevistas

Data de realização: 09 de setembro de 2008.

Margem de erro: 4,0 pontos percentuais para mais ou para menos.

Confiabilidade: 95,0% de confiabilidade.

Método amostragem: amostra não probabilística com determinações de cotas de sexo, idade e região de pesquisa.

Método de coleta das informações: abordagem sistemática da unidade respondente através do critério de sentido de fluxo X número aleatório X intervalo de coleta X enquadramento da cota, de modo a garantir o conceito de aleatoriedade.

Estatístico(a) Responsável: Fabíola Miranda von Rondow Inscrição N° 8140 - Série A

Diretores Responsáveis: José Luiz Soares Orrico / João Gualberto Moreira Vasconcellos

Registro: Cartório Eleitoral da 26a Zona do Município da Serra sob o nº 1.934/2008 , datado do dia 05 de setembro de 2008
.

ATENÇÃO: se uma pesquisa eleitoral divulgar uma previsão de intenção de votos, e no dia em que as urnas forem abertas o percentual ficar abaixo ou acima do intervalo de confiança estabelecido, isso não significa que a pesquisa tenha errado na previsão. Significa apenas que, caso trabalhe com um nível de confiança de 95%, o seu resultado, e isso é possível estatisticamente, tenha caído fora dos 95%. Ou seja, toda pesquisa tem uma chance de "errar", neste caso a chance foi de 5%. Repetindo, quando o cálculo dos votos de um candidato não bate com o de uma pesquisa de boca de urna não significa que ela tenha errado, ou melhor, que até tenha, mas que isto estava previsto estatisticamente.

.

¬ Lição matemática nº12: desvio-padrão

Desvio-padrão é a medida de dispersão mais empregada, por ser relativamente estável já que leva em consideração a totalidade dos valores da variável em estudo. Porém, sofre influência de valores extremos, assim como a média. Além disso, baseia-se nos desvios em torno da média aritmética.

Quanto maior for o desvio-padrão, maior será a variação entre os valores estudados (da população ou de uma amostra). Quanto menor for o desvio-padrão menor será a variação dos valores e, desta forma, esses valores serão mais homogêneos. Logo, quando o desvio-padrão é igual a zero não temos variações dos valores com relação à média, ou seja, eles são completamente homogêneos.

• Exemplo 1:

Pesos estudados:  5 5 5 5 5

Média aritmética = 5kg

Desvio padrão = 0

• Exemplo 2:

Pesos estudados: 8 9 10 11 12

Média aritmética = 10kg

Desvio padrão = 1,58kg

.

Notamos que no exemplo2 os pesos estudados variam mais do que os pesos do exemplo1, o que é fácil de identificar visualmente. Isso é demonstrado pelo desvio padrão de 1,58kg. Ou seja, os dados são heterogêneos, indo de8 a12kg. Logo, quanto maior o desvio padrão maior a heterogeneidade dos elementos analisados. Como exemplo, façamos uma outra simulação alterando para cima o último peso para verificarmos seus efeitos sobre a média e o desvio-padrão.

• Exemplo 3:

Pesos estudados: 8 9 10 11 52

Média aritmética = 18kg

Desvio padrão = 17kg

.

Como a média é influenciada por valores extremos, e esta acaba influenciando o desvio-padrão, notamos que ambos cresceram de forma relevante.

A fórmula básica do desvio-padrão pode ser traduzida como: somatório da raiz quadrada da média aritmética dos quadrados dos desvios e é representada por S. Logo,

S = √∑ (x_i-X)²+ (x_ii-X)²

               n - 1

onde:

x_i = dados da série

X = média da série

n = número de elementos da amostra (para calcularmos o desvio padrão de toda a população utilizaríamos n ao invés de n - 1)

Ex: Calcular o desvio padrão da amostra de uma população (preços) representada por $4, $3, $1, $2 ,$5

X	média	( X - média  )	(X - média )2
4	3	1	1
3	3	0	0
1	3	-2	4
2	3	-1	1
5	3	2	4
		Total	10

Sabemos que n = 5 - 1, logo  10 / 4 = 2,5.

A raiz quadrada de 2,5 é o desvio padrão = $1,58.

* A unidade na qual o desvio padrão é expresso é a mesma dos dados originais, ou seja, se os dados são em Reais, o desvio padrão também será em reais

Vejamos abaixo um exemplo de aplicação do desvio-padrão a partir de um artigo falando sobre o critério de seleção em algumas universidades.

"Desvio Padrão – Texto Vest Unicamp

Durante os 11 anos de escolaridade regular que antecedem o vestibular, os professores corrigem as provas e fornecem os resultados aos seus alunos em graus que, normalmente, variam numa escala de 0 (zero) a 10 (dez). São os chamados “graus brutos” que são facilmente entendidos por todos. Desta forma, se um aluno disser que tirou 10 (dez) em História, saberemos que ele acertou a prova toda. Por outro lado, se o mesmo aluno afirmar que tirou 5 (cinco) em Biologia, imaginaremos que ele acertou metade da prova. Tudo simples e fácil de entender!

Entretanto, chegada a hora do vestibular, os graus brutos a que estamos acostumados cedem lugar às notas padronizadas. E aí os estudantes fazem muitas perguntas. O que é uma nota padronizada? Como se faz para calculá-la? Por que não se podem usar as tradicionais notas brutas no vestibular? Nós, como professores e conhecedores das boas técnicas de avaliação, não podemos nos furtar a respondê-las.

As notas que são atribuídas na escola servem para verificar em que pontos da matéria o aluno está bem, em que partes ele precisa de reforço, se ele pode ser promovido de uma série para outra, se deve se submeter a um processo de recuperação e, finalmente, se deve ser reprovado. Nesta situação, caso o professor venha a “dar” 6 (seis) para um aluno e 8 (oito) para outro, em nada afetará a aprovação de ambos, nem interferirá na vida dos demais alunos. Em outras palavras, a nota na escola de primeiro e segundo graus não tem sentido comparativo, já que a aprovação ou a reprovação de um estudante não interfere na vida dos seus colegas. Mas no vestibular é diferente, pois a realidade atual impõe um sistema de comparação de notas, pois não há vagas para todos. Enquanto que na escola todos podem ser aprovados, no vestibular todos podem obter a nota mínima, mas somente os de melhor desempenho (maiores notas) ocuparão as vagas oferecidas. É a dos mais aptos pelo sistema do mérito intelectual.

E por que não podemos somar 8 (oito) de Matemática com o 8 (oito) de História no vestibular? Pela simples razão de que as provas não possuem o mesmo grau de dificuldade, já que, por exemplo, um 8 (oito) numa prova de Matemática que “teve” média 4 (quatro) vale mais do que um 8 (oito) numa prova de História que “teve” média 7 (sete)! Neste caso, a soma do 8 (oito) em Matemática com o 8 (oito) em História significa a mesma coisa que as seguintes somas: soma de 8 (oito) bananas com 8 (oito) laranjas! Soma de 8 (oito) centímetros com 8 (oito) polegadas! Soma de 8 (oito) litros com 8 (oito) galões! Um verdadeiro absurdo, não acham?

Para que duas ou mais parcelas sejam somadas é preciso que elas estejam numa mesma escala. Daí, a necessidade da padronização que utiliza a média e o desvio-padrão. E o que é desvio-padrão?  Desvio-padrão é uma medida do grau de dispersão dos resultados em torno da média, isto é, um número que mede o quanto os graus estão mais ou menos dispersos em relação à média. Exemplificando: se a maioria das notas de uma prova está nas proximidades da média, o desvio é pequeno, e se, num outro caso, as notas estão bastante espalhadas e distantes da média, o desvio é grande. E qual é a importância do desvio-padrão? Imaginemos que um aluno tire 7 (sete) numa prova de Física que “teve” média 4 (quatro) e 7 (sete) numa prova de Química que também “teve” média 4 (quatro). Qual o 7 (sete) que vale mais, o de Física ou de Química?

À primeira vista fica parecendo que os dois setes valem a mesma coisa, mas isto não é verdade. Vejamos porque. Imagine ainda que na prova de Física quase todos os graus estejam muito próximos da média (desvio pequeno) e que na prova de Química os graus estejam mais espalhados (desvio maior). Agora sim poderemos afirmar qual é o 7 (sete) que vale mais, pois o 7 (sete) em Física está situado acima de um maior número de notas que o 7 (sete) em Química. Em outras palavras, o 7 (sete) de Química não está tão afastado dos demais graus como o 7 (sete) em Física. Desta forma o 7 (sete) em Física “vale” mais. E como então poderemos calcular se uma nota “vale” mais ou menos que outra? Pelo cálculo da nota padronizada que traduz todas as notas para uma mesma escala, onde todas as provas, depois do tratamento matemático terão a mesma média e o mesmo desvio-padrão, isto é, terão o mesmo grau de dificuldade e a mesma distribuição de notas em torno da média. O cálculo é simples: diminui-se a nota que o aluno tirou da média da prova. Em seguida, divide-se o resultado pelo desvio-padrão e multiplica-se por 100. Finalmente, soma-se 500 a este último resultado e obtém-se a nota padronizada.

Esta nota padronizada pode ser somada às notas padronizadas de outras disciplinas porque estão na mesma escala. É por isso que a Unicamp, a Uerj, a UFF, a Fundação Cesgranrio, a PUC/RJ, a Access e a Fundação Carlos Chagas, entre outras, padronizam as notas dos vestibulares que realizam para que a seleção seja a mais justa possível. Pela mesma razão as grandes universidades dos países do primeiro mundo também se utilizam do método de padronização que foi popularizado no início do século pelo Colege Entrance Examination Board (USA)".

A partir do texto acima vamos a um exemplo:

Dois alunos fizeram provas de dois conteúdos no vestibular. O primeiro tirou 7 em uma e 7 na outra, ou seja, tem 14 pontos. O segundo tirou 10 em uma e 4 na outra, também com 14 pontos. Será que estão empatados? Se as notas forem padronizadas veremos que não.

Imaginemos que a média geral na primeira prova tenha sido 4, e a média da segunda 5. Porém, o desvio padrão da primeira tenha sido de 1 ponto, e da segunda 3 pontos. Ou seja, as notas estão mais afastadas no segundo caso e mais próximas no primeiro. Usando a metodologia do texto façamos uma simulação:

Aluno A (nota 1): 7,0

Desvio da média = 3 (7-4)

Desvio/desvio padrão = 3/1 = 3

3 x 100 = 300 + 500 = 800

Aluno A (nota 2): 7,0

Desvio com relação à média =  2 (7-5)

Desvio/desvio padrão = 2/3 = 0,666

0,66 x 100 = 66 + 500 = 566

Total de pontos = 1.366 (800 + 566)

                       

Aluno B (nota 1): 10,0

Desvio da média = 6 (10-4)

Desvio/desvio padrão = 6/1 = 6

6 x 100 = 600 + 500 = 1.100

Aluno B (nota 2): 4,0

Desvio com relação à média = -1 (4-5)

Desvio/desvio padrão = -1/3 = -0,33

-0,33 x 100 = -33 + 500 = 467

Total de pontos = 1.567 (467 + 1.100)

.

Ou seja, pela padronização das notas o Aluno B está na frente, pois foi bem em uma prova em que todo mundo foi mal, cuja média foi 4,0. Isto é, como nesta avaliação as notas estavam mais próximas de 4,0 (desvio - 1) e ele tirou 10, isso acabou favorecendo sua pontuação, uma vez que se destacou da maioria.

O Desvio padrão e a curva normal

O desvio padrão é utilizado também para indicar a dispersão dos dados dentro da amostra, isto é, o quanto os dados em geral estão distantes (diferem) da média. Quanto menor o desvio padrão, mais parecidos são os valores da amostra. Logo, por exemplo, quando uma série X  tem o mesmo número de dados de Y, e ambas tem a mesma média, se o desvio padrão de X for maior que de Y,  isso indica que os dados em X estão mais afastados da média que em Y.

Estudos estatísticos repetitivos mostram que numa distribuição de dados qualquer, quando o desvio padrão é calculado, temos uma ideia de onde estão localizados os valores da amostra, em torno da média. As conclusões são que:

68,26% dos valores da série (amostra) estão a até 1 desvio padrão de distância da média, isto é, estão entre  X - S   a   X + S

95,44% dos valores da série (amostra) estão a até 2 desvios padrão de distância da média, isto é, estão entre  X - 2S   a   X + 2S

99,73% dos valores da série (amostra) estão a até 3 desvios padrão de distância da média, isto é, estão entre  X - 3S   e   X + 3S

.

Imaginemos uma série estatística (amostra) relativa a alguma medida de uma população, peso dos alunos, por exemplo. Imaginemos que a média dessa amostra seja X = 100kg e desvio padrão S = 10Kg. De acordo com as afirmações acima, podemos inferir sobre a população, a partir da amostra selecionada, que:

68,26% dos alunos da amostra têm pesos entre 90kg (100 - 10) e 110kg (100 + 10)

95,44% dos alunos da amostra têm pesos entre 80kg (100 - 2 x 10) e 120kg (100 + 2 x 10)

99,73% dos alunos da amostra situam-se entre 70kg (100 - 3 x 10) e 130kg (100 + 3 x 10)

.

A figura abaixo mostra a curva normal e ilustra bem que vimos acima:

.

Veremos na lição seguinte a importância dessa curva normal e do desvio padrão no cálculo do tamanho da amostra e na interpretação do resultado de uma pesquisa quantitativa.

.

¬ Lição matemática nº11: medidas estatísticas (média, mediana e moda)

A ideia de escrever um post sobre as medidas estatísticas veio de um discussão, entre jornalistas, que teve um relativo murmurinho na mídia impressa e online. Tratou-se de uma critica escrita, em set/2011, pelo jornalista econômico Luiz Nassif em seu blog, cujo título foi A mídia abaixo da média. O artigo disserta sobre a dificuldade de os jornalistas interpretarem variáveis ou dados econômicos. A briga, propriamente dita, surgiu quando do resultado do Enad. Ele mostrava uma melhora nas médias dos alunos, o que deveria ser o foco explorado pelos jornalistas em suas manchetes on line no dia seguinte. Porém, não foi isso que se viu, falava-se apenas que os alunos ficaram, em sua maioria, abaixo da média, o que deu um tom um pouco pejorativo ao resultado do Enad. Aí veio o questionamento do Nassif. Dizia, com razão que por mais médias que tiremos de dados quaisquer teremos, na maioria das vezes, a maior parte dos dados abaixo da média da série e que, portanto, os jornalistas estavam 'chovendo no molhado' e perdendo o foco de suas reportagens. A falta de conhecimento mínimo da matemática fez com que eles se perdessem e, efetivamente, falassem bobagem. Como o assunto rendeu, o amplio aqui e vou um pouco além dessa medida mais comum, a média. Trato da média, mediana, moda, e em outro post, do desvio padrão.

As medidas de tendência central visam localizar o centro de um conjunto de dados, isto é, identificar um valor em torno do qual os dados tendem a se agrupar, sendo as mais utilizadas: média aritmética, mediana e moda. Também utilizarei a média ponderada por ser bastante interessante. Além disso trabalharemos com uma medida de posição importante (ou separatriz), denominada quartil.

a) MÉDIA ARITMÉTICA: é a medida de tendência central mais simples e conhecida. Mostra a soma de todas as observações (dados) dividida pelo número de observações.

Por exemplo, se uma empresa vende por dia 10, 14, 13, 15, 16, 18 e 12 kg, qual a venda média média diária na semana:

X = (10+14+13+15+16+18+12) / 7 =14 kg

.

Se os dados estiverem agrupados em uma distribuição de frequência o cálculo é similar. Consideremos a distribuição relativa à quantidade de filhos por família (domicílio) de determinada região carente.

Nº de filhos por família: 0, 8, 3, 2, 4, 1, 1, 3, 6, 3, 4, 9, 3, 7, 5, 5, 1

.

Nº de filhos	frequência = fi
0	1
1	3
2	1
3	4
4	2
5	2
6	1
7	1
8	1
9	1
total	17

A partir da tabela anterior temos:

X	f	X . f
0	1	0
1	3	3
2	1	2
3	4	12
4	2	8
5	2	10
6	1	6
7	1	7
8	1	8
9	1	9
total	17	75

onde 75 / 17 = 4,41 filhos por residência

Uma outra forma de agrupar dados facilitando sua visualização é ordená-los em intervalos de classe. Neste caso, teremos n elementos dentro de cada classe. E, se não dispusermos destes elementos individualmente, ainda assim, podemos achar a média a partir de um ponto médio da classe:

filhos	frequência  (f)	ponto médioX	X. f
0 -----| 2	5	1	5
2 -----| 4	6	3	18
4 -----| 6	3	5	15
6 -----| 8	2	7	14
8 -----| 10	1	9	9
Total	17	-	61

.
X = 61/17 = 3,58 filhos por residência

Notem que essa é uma média aproximada, já que consideramos pontos médios no cálculo, e não os valores originais. Assim, ganhamos em visualização, posto que a tabela fica menor, e perdemos um pouco em precisão.

b) MÉDIA PONDERADA: A fórmula anterior para calcular a média aritmética supõe que cada observação tenha a mesma importância. Ou seja, se tiramos a média de 2 números cada um deles tem peso 50%; se são 4 números o peso de cada um será igual a 20%. Já a média ponderada considera que as informações não têm a mesma importância, ou seja, devem ser levados em conta seus respectivos pesos. Assim, cada valor será ponderado (multiplicado) pelo peso a ele atribuído, e depois somados aos outros valores e seus respectivos pesos.

Consideremos que um professor informe a classe de que haverá dois exames parciais, valendo cada um 30% da nota e um exame final valendo 40%, portanto, 3 notas. Um aluno obtém 7 na primeira avaliação, 6,5 na segunda e 8,0 no exame final. Qual a média final do aluno?

Média ponderada final = 7,0 x 0,30 + 6,5 x 0,30 + 8,0 x 0,40  = 7,25

                                           0,30 + 0,30 + 0,40 (=1)                    

ou

Média ponderada final = 7,0 x 3 + 6,5 x 3 + 8,0 x 4  = 72,5

                                              3 + 3 + 4 (=10)      

ou

Média ponderada final = 7,0 x 30 + 6,5 x 30 + 8,0 x 40  = 725,0

                                           30 + 30 + 40 (=100)                      

Observem que o denominador é igual a soma das ponderações, ou seja, 100%. Se trabalharmos, como acima, no numerador com a porcentagem já transformada nosso denominador será sempre 1, o que nos poupa de uma conta adicional.

c) MODA: é o valor que ocorre com maior frequência em uma série de dados, ou seja, é o número que mais se repete. Desse modo, o salário modal dos empregados de uma fábrica é o salário mais comum, isto é, o salário recebido pelo maior número de empregados dessa fábrica.

Ex: Na série (7 , 8 , 9 , 10 , 10 , 10 , 11 , 12) a moda é igual a 10.

.
Há séries nas quais não existe valor modal, isto é, nenhum valor aparece mais do que outros.

Ex: (3 , 5 , 8 , 10 , 12) não apresenta moda. A série é amodal.

 .

Em outros casos pode haver dois ou mais valores. Dizemos, então, que a série tem dois ou mais valores modais.

Ex: (2 , 3 , 4 , 4 , 4 , 5 , 6 , 7 , 7 , 7 , 8 , 9) apresenta duas modas: 4 e 7.  A série é bimodal.

.

Uma vez agrupados os dados, é possível determinar imediatamente a moda, que é o valor da variável de maior frequência. No exemplo anterior a moda seria 3 (filhos), pois 4 das 17 famílias possuem 3 filhos. Para essa mesma tabela distribuída em classes a classe modal seria 2 -----| 4. Notem que neste caso não temos um valor da moda por não termos os valores originais. São 6 números entre 2 e 4, mas não os temos, sabemos apenas que esta classe se repete 6 vezes. Podemos, neste caso, determinar uma moda estimada que é exatamente o ponto médio da classe, 3. É como se o número 3, que representa a classe, se repetisse 6 vezes.

.

filhos	frequência  (f)	ponto médioX	X. f
0 -----| 2	5	1	5
2 -----| 4	6	3	18
4 -----| 6	3	5	15
6 -----| 8	2	7	14
8 -----| 10	1	9	9
Total	17	-	61

.

d) MEDIANA: a mediana de um conjunto de valores, dispostos segundo uma ordem (crescente ou decrescente), é o valor situado de tal forma no conjunto que o separa em dois subconjuntos de mesmo número de elementos., ou seja, 50% acima e 50% abaixo da mediana.

Dada uma série de dados não agrupado (5, 2, 6, 13, 9, 15, 10), de acordo com a definição de mediana, o primeiro passo a ser dado é o da ordenação (crescente ou decrescente) dos valores (2, 5, 6, 9, 10, 13, 15). O valor que divide a série acima em duas partes iguais, mediana, é igual a 9.

Se a série dada tiver número ímpar de termos o valor mediano será o termo de ordem dado pela fórmula: (n + 1)/2

Ex: Calcule a mediana da série (10, 7, 6, 8, 5, 5, 3)

1º  ordenar a série (3, 5, 5, 6, 7, 8, 10)

n = 7 logo (n + 1)/2 é dado por (7+1)/2 = 4,

ou seja, o 4º elemento da série ordenada será a mediana, o número 6.

.

Se a série dada tiver número par de termos o valor mediano será o termo de ordem dado pela média dos dois valores centrais.

Ex: Calcule a mediana da série (3, 5, 5, 6, 7, 8, 9, 9)

A mediana no exemplo será a média aritmética do 4º e 5º termos da série, ou seja, (6+7)/2 = 6,5.

.

Para dados agrupados em distribuição de frequência basta identificar a frequência acumulada imediatamente superior à metade da soma das frequências. A mediana será aquele valor da variável que corresponde a tal frequência acumulada. Na nossa tabela inicial de nº de filhos a mediana seria o 9º elemento [(17+1)/2]. Basta contar na coluna da frequência que encontramos o 9º elemento, o número 3 (filhos).

Se a tabela estivesse na forma de intervalos de classe faríamos o mesmo procedimento acima, sendo que o valor da mediana agora estaria dentro da classe de preços. O 9º elemento estaria na classe de 2 a 4. Como vimos, já que não temos um valor podemos utilizar o valor médio como estimativa, ou seja, o 3. Neste caso de distribuição em classes, mediana e moda coincidiram.

filhos	frequência  (f)	ponto médio X	X. f
0 -----| 2	5	1	5
2 -----| 4	6	3	18
4 -----| 6	3	5	15
6 -----| 8	2	7	14
8 -----| 10	1	9	9
Total	17	-	61

Notas:

• Em uma série a mediana, a média e a moda não têm, necessariamente, o mesmo valor.


• A mediana, depende da posição e não dos valores dos elementos na série ordenada, ao contrário da média.

Em ( 2, 5, 5, 6, 7) a média = 5 e a mediana = 5

Em ( 2, 5, 5, 6, 22) a média = 8 e a mediana  = 5

isto é, a média do segundo conjunto de valores é maior do que a do primeiro, por influência dos valores extremos, ao passo que a mediana permanece a mesma.

• Utilizamos a mediana quando há valores extremos que afetam de maneira acentuada a média aritmética. Os relatórios do Banco Central, por exemplo, ao consultarem analistas sobre as suas perspectivas da inflação, juro, etc, buscam evitar valores extremos dados pelas entrevistas, pois podem puxar pra cima o centro da série e deixar o mercado nervoso com sua divulgação. Nesse sentido, para fugir dos valores extremos o Bacen costuma tratar da mediana, como vemos no trecho da reportagem do Estadão de 09/09/13: "Com a divulgação do Índice Nacional de Preços ao Consumidor Amplo (IPCA) de agosto dentro do esperado, o relatório de mercado Focus, divulgado neta segunda-feira, 9, pelo Banco Central, sofreu um leve ajuste para baixo nas estimativas para o índice oficial de inflação no País para este ano. A mediana para o índice de 2013, passou de 5,83% para 5,82% ...".

.

Além das medidas de posição que estudamos há outras que, consideradas individualmente, não são medidas de tendência central, mas estão ligadas à mediana relativamente à sua característica de separar a série em duas partes que apresentam o mesmo número de valores. Essas medidas (os quartis e os decis) são conhecidas pelo nome genérico de separatrizes, ou medidas de posição. Vejamos a seguir 1 delas, os quartis.

e) QUARTIS (Q): denominamos quartis os valores de uma série que a dividem em quatro partes iguais.  Precisamos, portanto de 3 quartis (Q1 , Q2 e Q3) para dividir a série em quatro partes iguais. Logo, o quartil 2 ( Q2 ) sempre será igual a mediana da série.

Para dados não agrupados o método mais prático é utilizar o princípio do cálculo da mediana para os 3 quartis. Na realidade serão calculadas "3 medianas" em uma mesma série.

Ex1: Calcule os quartis da série: (5, 2, 6, 9, 10, 13, 15)

- O primeiro passo é a ordenação (crescente ou decrescente) dos valores: (2, 5, 6, 9, 10, 13, 15)

- O valor que divide a série acima em duas partes iguais é igual a 9, logo a Mediana = 9 = Q2 = 9

- Temos agora (2, 5, 6) e (10, 13, 15) como sendo os dois grupos de valores iguais proporcionados pela mediana (Q2). Para o cálculo do quartil 1 e 3 basta calcular as medianas das partes iguais provenientes da verdadeira Mediana da série (Q2).

Logo:

em (2, 5, 6) a mediana é = 5. Logo, será o quartil 1 (Q1 = 5)

em (10, 13, 15) a mediana é = 13. Logo, será o quartil (Q = 13)

Temos então: (2, 5, 6, 9, 10, 13, 15)

.
Ex2: uma pesquisa salarial mostra que o salário nominal de uma categoria está assim distribuído:
Q1 = R$ 2.057
Mediana (O2) = R$ 2.400
Q3 = R$ 3.500

Concluímos que 25% dos salários dessa categoria estão abaixo de R$2.057, 50% deles abaixo de R$2.400, e apenas 25% acima de R$3.500.

.

¬ Lição matemática n°10: Como calcular a rentabilidade (yield) de um título

O mercado internacional de dívidas permite o levantamento de recursos (dólares, ienes, euros etc) via emissão de títulos pelos tomadores: empresas, bancos ou governo.  A forma mais comum de captação são os bonds, ou bônus. São títulos de longo prazo representando uma dívida do emissor, como vimos na lição de economia nº26 sobre Risco-País. Podem pagar um juro fixo no vencimento ou  juros periódicos (anuais ou semestrais), denominados cupons, além da amortização do principal no vencimento da dívida. As taxas de juros embutidas podem ser fixas ou flutuantes, dependendo dos critérios definidos na emissão, sendo estas baseadas no valor em pontos que esteja o Risco-País no período.

O cálculo da rentabilidade desses bonds (YTM – yield to maturity) é determinado a partir do preço de mercado do título (preço de compra) e os fluxos de pagamento a ele associados, os cupons. Assim, se considerarmos o preço de mercado do Bond e os fluxos de pagamento, a sua taxa embutia de retorno (YTM) será exatamente a IRR (taxa interna de retorno) que vimos nas lições de matemática. Essa taxa, comparada com outras taxas no mercado, dirá se vale a pena para o investidor adquirir ou não o Bond. Temos, então, a seguinte fórmula:

 

P =       F1        +        F2         +   Fn  +  Vf

       (1+YTM)¹      (1+YTM)¹      (1+YTM)ⁿ

Onde:

P = preço de mercado do Bond

F1, F2 ...= fluxos de caixa ou pagamentos periódicos (cupons)

Vf = valor de face do papel ou valor nominal

N = períodos em que são pagos os cupons

YTM = taxa de juros que, descontados os fluxos de caixa, resulta em um valor presente igual ao preço de mercado. É a taxa de remuneração desejada pelo investimento feito.

Imaginemos um título já emitido e que esteja circulando no mercado secundário com valor de face de $1.000, que paga juros semestrais proporcionais a 10% ao ano. O prazo de resgate do titulo (maturity) é de 10 anos. Qual preço o investidor aceitaria pagar no mercado suponde as seguintes rentabilidades desejadas:

a) 5% ao semestre

P = 50/1,05 + 50/1,05² + ... + 50/1,05²⁰ + 1.000/10,5²⁰

P = $1.000

* Notamos  que o rendimento de 5% ao semestre é exatamente igual à taxa do cupom, e o preço do bônus é igual ao seu valor de face. Ou seja, se pagamos $1.000 no mercado por esse título teremos exatamente a rentabilidade semestral de 5%

b) 3% ao semestre

P = 50/1,03 + 50/1,03² + ... + 50/1,03²⁰ + 1.000/10,3²⁰

P = $1.297,55

* Neste caso, para conseguir o rendimento de 3% ao semestre o preço pago pelo bônus deve ser de $1.297,55. Isto é, se a exigência de rentabilidade diminui aceito pagar mais pelo Bond.

c) 6% ao semestre

P = 50/1,06 + 50/1,06² + ... + 50/1,06²⁰ + 1.000/10,6²⁰

P = $885,30

* Como o investimento requer uma rentabilidade de 6% preciso comprar o título com deságio no mercado, ou seja, um valor igual ou inferior a $885,30. Neste caso temos um deságio (queda) de 11,47% do valor de face [(885,30/1.000)-1].

d) rendimento de 6% supondo que o título já esteja circulando no mercado há 5 anos, ou seja, com 10 meses a menos de pagamento de cupons.

P = 50/1,06 + 50/1,06² + ... + 50/1,06¹⁰ + 1.000/10,6¹⁰

P = $885,30



* o deságio agora cai para 7,3% do seu valor de face.

Matematicamente, notamos que quando o valor do título no mercado diferir do valor nominal, o rendimento até o vencimento vai diferir da taxa de juros do cupom. Se o preço do título sobe no mercado o retorno (YTM) diminui, fica abaixo do cupom de lançamento. Se o título for negociada abaixo do valor nominal, com deságio, o YTM fica acima do cupom de lançamento. Neste caso, podemos também determinar o rendimento de um título a partir de seus preços e do cupom. Supondo um Bond com prazo de 2 anos que paga cupom de 5% ao semestre, um preço no mercado de $1.089 (ágio de 8,9% sobre o valor de face de $1.000), qual seria o seu rendimento?

Como o valor do título está com ágio, já sabemos que sua taxa de retorno será inferior à taxa do cupom de 5%.


1.089 = 50/(1+YTM) + 50/(1+YTM)² + 50/(1+YTM)³ + (50 + 1.000)/(1+YTM)⁴

YTM = 2,62% ao semestre



HP12c:

1089 (CHS) (PV) 50  (PMT) 4 (n) 1000 (FV) (i)?

R: 2,62%

Agora dá pra entender por que quando o mercado financeiro está nervoso e os investidores procuram títulos do governo como segurança, fugindo das bolsas de valores, seu valor de face sobe e o rendimento (YTM) fica abaixo do cupom - rendimento menor em função da maior demanda por segurança. Vejam como isso é descrito nos artigos online: "Aumento do pessimismo no mercado leva à alta dos preços dos Treasuries: Os preços dos Treasuries avançaram nessa quinta-feira após uma sequência de sete quedas seguidas, refletindo o pessimismo do mercado em relação à situação europeia devido à possível entrada do setor privado em planos de resgate da dívida da região. Desse modo, houve uma maior procura por ativos mais seguros no mercado, incluindo os títulos norte-americanos, o que levou a uma diminuição dos seus yields".

Analisemos a notícia abaixo da Gazeta Mercantil  de 16/10/2003-B1:


“Banco Central lança bônus de US$1,5 bilhão

O Banco Central anunciou ontem a emissão de US$1,5 bilhão em Global Bônus, com vencimento em outubro de 2010. A captação, que foi agenciada pelo Merrill Lynch e Credit Suice, gerou um cupom de 9,25% ao ano; a taxa de retorno para o investidor foi de 9,45% ao ano. Segundo nota do BC, o spread da operação foi de 561 pontos básicos acima dos títulos do Tesouro norte-americano de referência. Em setembro o BC emitiu US$775 milhões em Global Bônus com vencimento em agosto de 2011, e com isso atingiu a marca de US$3 bilhões em emissões no exterior que faziam parte do cronograma para 2003.

Taxa de retorno

Na ocasião, o cupom foi de 10% ao ano e o preço de reabertura da linha foi de 96,5% do valor de face. Com isso, a taxa de retorno para o investidor ficou em 10,66% ao ano. A linha BR-11 foi reaberta com spread de 6.333 pontos-básicos acima do título do Tesouro norte-americano de referência.

No final do mês passado, o diretor de política econômica, Afonso Bevilaqua, informou que o governo poderia emitir mais US$5 bilhões no prazo de 12 meses para aproveitar as boas condições de Risco-Brasil. Na terça-feira, a taxa de Risco-Brasil, medida pelo J.P. Morgan, chegou a bater em 579 pontos, menor patamar desde julho de 1998, o que aumentou as especulações no mercado financeiro sobre a iminência de uma nova emissão de bônus soberano”.

A matéria acima mostra a captação de recurso com a emissão de bônus por parte do governo federal. Traz também a rentabilidade para os investidores, os compradores dos bônus. A nova linha aberta em setembro pagou um cupom de 10% aa. Todavia, como a venda é feita em sistema de leilão, o valor de face negociado foi de 96,5%, o que dá ao investidor uma rentabilidade de 10,66% ao ano. A partir dos cálculos que fizemos anteriormente temos:

Deságio = 3,5%

P = US$96,50

Taxa de juro do cupom (equivalente) = 10% aa (4,8809% ao semestre)

F1, F2 ... (cupons semestrais) = US$4,88

Vf = US$100,00

n = 16 meses (8 anos, pois o vencimento é em 1011)



96,5 = 4,88/(1+YTM) + 4,88/(1+YTM)² + ... + (4,88 + 100)/(1+YTM)¹⁶

YTM = 5,20% ao semestre = 10,68% (equivalente anual)



HP12c:

96,5 (CHS) (PV) 4,88  (PMT) 16 (n) 100 (FV) (i)?

R: 5,20%

¬ Lição matemática nº9: Fluxos de caixa com prestações diferentes e as funções NPV e IRR da HP12c

Quando as prestações são diferentes, a tecla PMT não serve para os cálculos, pois ela supõe que as prestações sejam iguais. Existem, contudo, outras funções que permitem a inserção de prestações diferentes, desde que os fluxos de caixa sejam informados de forma seqüencial, sendo indispensável o registro de todas as parcelas do fluxo, inclusive as que tiverem valor igual a zero. Assim, na HP12c usamos a seguinte simbologia:

CF₀ – para registrar o fluxo de caixa do ponto zero

CF_j – para registrar o fluxo de caixa de um ponto médio

N_j – para registrar o numero de parcelas individuais (CF_j ) de mesmo valor e repetidas seqüencialmente.

Exemplos

1) Um investidor aplica seu dinheiro em um fundo de investimento. Faz quatro resgates mensais de respectivamente $ 1.000; $ 1.500; $ 3.000 e $ 2.750. Sabendo-se que esse fundo de investimento remunera suas aplicações a uma taxa de juros de 0,1% ao dia, qual o valor investido e qual o valor a ser resgatado por esse investidor no fim do quinto mês?

 

Conversão da taxa de diária para mensal.

i₃₀ = [(1 + 0,001)³⁰ -1] x 100

i₃₀ = 3,043%

Podemos resolver o problema descontando uma por uma das 4 prestações, depois de convertida a taxa, como se segue:

PV₀ = 1.000/(1,03043)¹  +  1.500/(1,03043)²  +  3.000/(1,03043)³  +  2.750/(1,03043)⁴

PV₀ = $ 7.564,00

* Este valor foi encontrado pela HP. Fazendo manualmente haverá alguma diferença em função dos arredondamentos.

Agora capitalizamos o valor até o mês 5.

FV₅ = PV₀ (1 + i)ⁿ

FV₅ = 7.564 (1,03043)⁵

FV₅ = $ 8.787,00

Poderíamos também capitalizar valor por valor até o mês 5 diretamente.

 FV₅ = 1.000(1,03043)⁴  +  1.500(1,03043)³  +  3.000(1,03043)²  +  2.750(1,03043)¹

Fv₅ = $ 8.787,00

Pela HP12C:

(f) (REG) 1.000 (g) (CF_j) 1.500 (g) (CF_j) 3.000 (g) (CF_j) 2.750 (g) (CF_j) 3,043 (i) (f) (NPV)

PV₀ = $ 7.564,00

* a tecla NPV traz o valor presente da série de prestações não uniformes.

(f) (REG) 7564 (CHS) (PV) 5 (n) 3,043 (i) (FV)

FV₅ = $ 8.787,00

2) Suponha que um investimento de $7.000 tenha uma expectativa de retorno de $3.000, $2.000 e $2.500 nos três meses seguintes. Calcule a taxa de retorno desse investimento.

 

7.000 = 3.000/(1 + i)¹  +  (2.000)/(1 + i)²  +  2.500/(1 + i)³

Pela calculadora financeira temos:

(f) (REG) 7.000 (CHS) (g) (CF₀) 3.000 (g) (CF_j) 2.000 (g) (CF_j) 2.500 (g) (CF_j) (f) (IRR)

i =  3,658% am

 * a tecla IRR é similar a tecla i, sendo utilizada quando as séries (prestações) são irregulares, diferentes.

Manualmente, a taxa pode ser encontrada de forma aproximada por interpolação linear. Escolhemos duas taxas, aleatoriamente, que impliquem um PV maior, e outro menor que 7.000, para fazermos a interpolação.

Para i = 1% temos: PV = 2.970 + 1.960 + 2.426 = 7.356

Para i = 3% temos: PV = 2.912 + 1.885 + 2.287 = 7.084

Para i = 4% temos: PV = 2.884 + 1.849 + 2.222 = 6.955

  

3) Uma empresa investirá 100.000 em um projeto voltado à exportação que lhe proporcionará lucros de $ 40.000 no primeiro ano, $ 50.000 no segundo ano e $ 60.000 no terceiro ano. É estimada uma desvalorização do dólar de 20, 25 e 30%, respectivamente, o que elevará os lucros da empresa nestes anos. Todavia, é estimada uma inflação no período de 22, 28 e 35%. Qual a taxa de retorno real deste investimento?

EQUIVALÊNCIA DE FLUXOS DE CAIXA

Dois fluxos de caixa são equivalentes, a uma determinada taxa de juros, se seus valores presentes (PV), calculados com essa mesma taxa de juros, forem iguais em qualquer data focal. Da mesma forma, se os fluxos de caixa tiverem o mesmo valor presente, a uma determinada taxa de juros, então seus valores futuros (FV) após n períodos, obtidos com essa mesma taxa de juros, são necessariamente iguais.

 Exemplos

1) Os quatro fluxos de caixa a seguir são equivalentes para uma taxa de juros de 5% ao mês? Considere duas datas focais, em t₀ e t ₁₈.

 

190/(1,05)² = 220/(1,05)⁵ = 267/(1,05)⁹ = 414/(1,05)¹⁸

172 = 172 = 172 = 172

2) Uma pessoa deve $ 3.000 com vencimento em 2 anos e $ 4.500 com vencimento em 6 anos. Pretende pagar seus débitos por meio de um pagamento único a ser efetuado no final de 4 anos. A juros de 10% aa, calcular o valor do pagamento único que liquida a dívida.

 

FV₄ = 3000 (1,1)²  +  4500/(1,1)²

FV₄ = $ 7.349,00

¬ Lição matemática nº8: Fluxos de caixa com prestações iguais

Todas as entradas e saídas monetárias podem ser expressas por uma linha horizontal que mostra o movimento de um capital ao longo do tempo. A essa linha damos o nome de fluxo de caixa, e dentro do mesmo estão representadas as entradas e saídas monetárias no tempo. Podemos ter fluxos de caixa de empresas, de investimentos, de projetos, de operações financeiras, etc.

 

                                           

Os fluxos de caixa possuem diversas formas e tipos em termos de períodos de ocorrência (postecipados, antecipados ou diferidos), de periodicidade (períodos iguais entre si ou diferentes), de duração (limitados ou indefinidos) e de valores (constantes e variáveis). O fluxo de caixa padrão (que veremos nesta lição) possui as seguintes das características acima: pagamento (ou recebimento) postecipado, prazo total limitado, valores constantes e intervalos de pagamentos periódicos. Esses pagamentos constantes e periódicos do fluxo de caixa são denominados  prestações, ou PMT (payment) na HP12C.

Nesta lição falaremos dos fluxos padrão e destes com séries antecipadas e postecipadas. Na lição seguinte (nº 9) trataremos apenas dos fluxos de caixa não convencionais comprestações diferentes e a função NPV da HP12c.

Exemplo do fluxo de caixa padrão:

Fórmulas para o fluxo de caixa padrão:

Onde, 

é o fator de capitalização, e








o fator de descapitalização



EXEMPLOS

1) Determinar o valor do principal de um financiamento realizado com uma taxa efetiva de 1% ao mês, em juros compostos, e que deve ser liquidado em 12 prestações mensais, sucessivas e iguais a $1.000.

PV = 1.000 [1 – 1/(1 + 0,01)¹²]/0,01

PV = $11.255,00



(f) (REG) 1.000 (CHS) (PMT) 12 (n) 1 (i) (PV)?

PV = $11.255,00

2) Determinar o valor presente (PV) de um fluxo de 12 pagamentos trimestrais, iguais e sucessivos de  $700,0, sendo a taxa de juros igual a 1,7% ao mês.

Como a taxa de juros é mensal mas os pagamentos trimestrais, temos inicialmente que transformá-la para uma taxa trimestral.

i₉₀ = [(1 + 0,017)^90/30 –1] x 100

i₉₀ = [(1,017) ³ –1] x 100

i₉₀ = 5,18%



(f) (REG) 1,017 (ENTER) 90 (ENTER) 30 (÷) (Y^x) 1 (-) 100 (x)

i = 5,18%



Calculando o PV:

PV = PMT [1- 1/(1 + i)ⁿ]/i

PV = 700 [1 – (1/(1 + 0,0518)¹²)]/0,0518

PV = 700 x [(1 – (0,5455)]/0,0518

PV = $ 6.141,00



(f) (REG) 5,18 (i) 700 (CHS) (PMT) 12 (n) PV?

PV = $6.140,00

3) Um financiamento de $ 3.500,00 é concedido a juros de 2,5% ao mês. Podendo-se dispor de $ 270,00 ao final de cada mês, determinar quantos pagamentos são necessários para liquidar o empréstimo.

 3500 = 270 [1 – 1/(1 + 0,025)ⁿ]/0,025

[FATOR] = 12,96

Para um juro de 2,5% e um fator de 12,96 (fator de valor presente) a tabela financeira nos dá um prazo de 16 meses (pagamentos).

Já vimos em exercícios anteriores como determinar o n matematicamente. Assim, caso não dispuséssemos da tabela financeira poderíamos fazer da seguinte forma:

3500 = 270 [1 – (1,025)ⁿ]/0,025

12,96 = [1 – (1,025)ⁿ]/0,025

[1 – (1,025)ⁿ ] = 12,96 x 0,025 = [1 – (1,025)ⁿ ] = 0,32413,28

- (1,025)ⁿ = 0,324 – 1

n log 1,025 = log 0,676

n = log 0,676/log 1,025 = -0,03915/0,002469

n = 15,85 meses



 (f) (REG) 2,5 (i) 3500 (CHS) (PV) 270 (PMT) (n)?

n =15,85 meses

4) Um eletrodoméstico é vendido à vista por 8.000 à vista ou em 1 entrada mais 4 pagamentos mensaid de $2.085,89, sendo o primeiro pagamento 3 meses após a compra. Qual deve ser o valor da entrada considerando uma taxa de juros de 4% ao mês?

Sabemos que se calcularmos o PV na fórmula padrão é como se o tempo 2 funcionasse no tempo zero, pois a primeira prestação é sempre postecipada. Logo, como o PV padrão cairia no tempo 2 bastaria descapitalizar o principal encontrado por mais dois períodos para termos seu  valor no tempo zero.

 

Fluxo padrão (PV no tempo 2):

PV = PMT [1- 1/(1 + i)ⁿ]/i

PV₂ = 2085,79 x [1 – 1/(1 + 0,04)⁴]/0,04

PV₂ = 2085,79 x 3,6298

PV₂ = 7.569,00

PV descontado por 2 períodos (PV em zero):

PV₀ = PV₂/(1,04)²

PV₀ = 7.568,32/(1,04)²

PV₀ = $ 6.997,00

(f) (REG) 4 (i) 2085,79 (CHS) (PMT) 4 (n) PV?

PV₂ = $ 7.571,00

(f) (REG) 4 (i) 2 (n) 7571 (CHS) (FV) PV?

PV₀ = $ 6.999,00

Sabemos que: valor a vista = entrada + valor a ser financiado (valor presente). Como o valor presente das prestações deve ser igual ao valor a vista (8.000), temos:

ENTRADA = 8000 – 7000 = $1.000,00.

5) Um empréstimo de $10.000 será liquidado em 2 vezes iguais. Sabendo-se que a taxa cobrada é de 3% ao mês, determine o valor das parcelas.

                           

10.000 = PMT/(1+0,03)¹ + PMT/(1+0,03)²

10.000 = PMT/(1,03) + PMT/(1,06)

10.000 = PMT (0,9708) +  PMT(0,9425)

10.000 = 1,9133 PMT

PMT = $5.226,00



(f) (REG) 10000 (CHS) (PV) 2 (n) 3 (i) (PMT)

PMT = $5.226,00

6) Uma pessoa financia um carro de $20.000,00 em 24 vezes, sendo cobrada uma taxa de IOC de 1,5% (sobre o valor do contrato) e uma TAC de $ 150,00. Ambas serão embutidas nas prestações. A taxa de juros cobrada no empréstimo é de 2,7% am. Pede-se: a) o valor das prestações mensais, b) e a taxa efetiva de juros deste financiamento. c) o valor financiado e o valor total pago incluindo o custo de oportunidade.

Valor total financiado (PV): 20.000 + 300,00 (20.000 x 1,5%) + 150,00 = $20.450,00

i: 2,7% am

período: 24 meses

PMT: ?

a) 20.450 = PMT [1 - 1/(1 + 0,027)²⁴]/0,027

20.450 = PMT [17,496] – fator de descapitalização

PMT = 20.450/17,49609

PMT = $ 1.169,00



(f) (REG) 2,7 (i) 24 (n) 20450 (CHS) (PV) (PMT)?

PMT = $ 1.169,00

b) Como incluímos no valor financiado as taxas a serem pagas (caso as pagássemos no ato o raciocínio seria parecido) temos que verificar qual a taxa efetiva do financiamento, que certamente será superior aos 2,7% am.

Como o principal é de $20.000 e as prestações (que incluem as taxas) $1.169, temos que jogar esses dados na fórmula para determinar a taxa embutida:

20.000 = 1.169 [FATOR]

20.000/1.169 = [FATOR]

[FATOR] = 17,10

Pela tabela (PV/PMT  para 24 meses) encontramos uma taxa de aproximadamente: 2,89%

(f) (REG) 24 (n) 20000 (CHS) (PV) 1169 (PMT) (i)?

i = 2,90% 

Logo, a taxa efetiva, incluindo as despesas com as demais taxas, é de 2,89%, superior aos 2,7% do contrato. Qualquer taxa adicional tende, portanto, a encarecer o custo do financiamento.

c) Calculando FV (valor futuro) temos:

FV = PMT [(1 + i)ⁿ - 1 ]/i                     

FV = 1169 [((1,027)²⁴ -1)]/0,027

FV = 1169 x 33,16

FV = $38.765 (valor total do financiamento)

(f) (REG) 2,7 (i) 24 (n) 1169 (CHS) (PMT) (FV)?

FV = $ 38.765 

Uma observação deve ser feita. O valor efetivamente pago por quem tomou o financiamento foram as 24 prestações de $ 1.169. Logo, somando-se encontramos um total de $28.056 ($ 1.169 x 24). Mas se esse foi o valor pago o que significa aquele valor futuro de $38.765, bem superior?

O valor efetivamente desembolsado foram os $28.056, mas pensando de outra forma, se você emprestasse $20.000 reais a alguém e recebesse as prestações de $1.180 o que faria com elas? Se emprestou é porque este dinheiro estava de certa forma sobrando. Logo, assim que for recebendo as prestações de $1.169 irá aplicá-las, supondo a mesma taxa do financiamento, ao longo dos 24 meses. Assim, receberá $28.056 na forma de prestações e ganhará um rendimento extra pelas aplicações de $10.709 (38.765 - 28.056). É exatamente isso que o banco faz quando concede empréstimos, reaplica as prestações (ou as empresta a outro) assim que elas forem sendo pagas.

Conclusão, como receberia as prestações mensais, mas não as deixaria paradas, ao reaplicá-las no mercado, à mesma taxa, recebe um total de $38.765, que é exatamente aquele valor futuro calculado pela fórmula. Nesse sentido, a matemática financeira considera não só o custo do seu financiamento, mas o custo de você ter disponibilizado o dinheiro pelo tempo especificado e não ter recebido nada com isso (custo de oportunidade). Esse custo adicional é somado ao valor das prestações que pagará. Assim, o valor total despendido seria de $ 38.765, e não apenas os $28.056.

7) Uma empresa precisa de capital de giro. Porém, de acordo com seu fluxo de caixa só poderá liquidá-lo em cinco parcelas mensais postecipadas de $2.500, com um período de carência de 15 dias. Calcular a capacidade da empresa de tomar empréstimo, sabendo-se que a taxa de juro da operação é de 12% ao ano.

i_mensal = (1,12)^1/12 -1 = 0,9489% ao mês

PV = 2500 [1 – 1/(1,009489)⁵]/0,009489

PV = 12.151/(1,0047)

PV = 12.094



(f) (REG) 0,9489 (i) 5,5 (n) 2500 (CHS) (PMT) (PV)?

PV = $12.094 

8 ) Um veículo à vista custa $20.000. Em um consórcio, a taxa de administração paga é de 5% am e as prestações mensais de $600, ao longo de 60 meses. Qual a taxa efetiva mensal da operação?

PV = 20.000

N = 60 meses

PMT = 600 x Tx adm = 630

i?

20.000 = 630 [1 - 1/(1+i)⁶⁰]/i

fator = 57,97

(f) (REG) 20000 (CHS) (PV) 60 (n) 630 (PMT) (i)?

i = 2,38% am 

9) Um equipamento é vendido à vista por $40.000, ou em três prestações mensais fixas. Calcular o valor das prestações considerando uma taxa de juros real aplicada de 5% am, e inflação projetada de 1%am.

i = (1,05) x (1,01) = 6,05% am

40.000 = PMT [1 - 1/(1,0605)³]/0,0605

40.000/2,67 = PMT

PMT = $ 14..978



(f) (REG) 40000 (CHS) (PV) 6,05 (i) 3 (n) (PMT)?

PMT = 14.980 

FLUXOS DE CAIXA NÃO CONVENCIONAIS (séries antecipadas e postecipadas)

Como vimos, os fluxos não convencionais podem ser classificados como antecipados, diferidos (carência), valores (prestações) diferentes (este veremos especificamente na lição 9).

No fluxo antecipado a série de valores (prestações) começa a ocorrer antes do final do primeiro período, ou no início deste. Quando tratamos de carência (postecipado) estamos falando de uma série de pagamentos que começa a ocorrer após o primeiro período, já que o pagamento no primeiro período é classificado como fluxo padrão, como vimos. Da mesma forma, quando os períodos de pagamento, e/ou os valores são diferentes, também temos um fluxo de caixa não convencional.

Exemplo de um fluxo de caixa com carência de um período:

Exemplo:

Um financiamento de $1.000,00 deve ser amortizado em cinco prestações mensais, iguais e sucessivas. Sabendo-se que a taxa efetiva de juros é de 1% ao mês, e admitindo-se meses com 30 dias, determinar o valor da prestação mensal desse financiamento, nas seguintes hipóteses:

i) pagamento da 1ª prestação ocorrendo um mês após a liberação dos recursos (série postecipada -padrão);

ii) pagamento da 1ª prestação (entrada) ocorrendo no ato da liberação dos recursos (série antecipada).

i) Fluxo padrão:

1.000 = PMT [1 - 1/(1 + 0,01)⁵]/0,01

1.000 = PMT [4,8534] – fator de descapitalização

PMT = 1.000/4,8534

PMT = $206,04



(f) (REG) 1 (i) 5 (n) 1000 (CHS) (PV) (PMT)?

PMT = $ 206,04 



ii) Esse é um fluxo de caixa antecipado, logo:

Como a prestação inicial (de um total de 5) é paga no tempo zero, o principal é a soma desta entrada mais as outras 4 prestações restantes, podendo considerar estas como um fluxo padrão.

PV = PMT (entrada) + PMT [1- 1/(1 + i)ⁿ]/i

1.000 = PMT + PMT [1- 1/(1 + 0,01)⁴]/0,01

1.000 = PMT + PMT [3,901]

1.000 = 4,901 PMT

PMT = 1.000/4,901

PMT = $203,99



(f) (REG) (g) (BEG) 1 (i) 5 (n) 1000 (CHS) (PV) (PMT)?

PMT = $ 203,99

* a HP12c trabalha com séries antecipadas ao pressionamos as teclas (g), tecla azul,  e (BEG), de begin. Para voltarmos ao fluxo de caixa padrão pressionamos (g) e depois (END).